ماتریسەکان دەورێکی سەرەکی لە جەبری هێڵیدا دەگێڕن. دەکرێت بۆ نواندنێکی چڕی سیستمەکانی هاوکێشە هێڵییەکان کەڵک لە ماتریسەکان وەربگرین. هەروەها دەکرێت بۆ نواندنی نەخشە هێڵییەکانیش کەڵکیان لێ وەربگرین. بەر لەوەی کە بە وردی ئەو باسە سەرنجڕاکێشانە وەرد بدەینەوە با سەرەتا ماتریس پێناسە بکەین و ڕوونی بکەینەوە کە چ کردارێک لەسەر ماتریس جێبەجێ دەکرێت.

پێناسە: ماتریس

بە هەبوونی $m, n \in \mathbb{N}$، ماتریسێک لە بڕە ڕاستییەکان $(m, n)$ $A$ بریتییە لە $m \times n$-تاپڵ لە ئەندامەکانی $a_{ij}$, کە $i = 1, \dots, m$ و $j = 1, \dots, n$, بە شێوەیەکی لاکێشەیی لە $m$ ڕیز و $n$ ئەستووندا ڕێک دەخرێن:

$$A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix}, \quad a_{ij} \in \mathbb{R}.$$

بەپێی گرێبەست، بە ماتریسەکانی $(1, n)$ ڕیز دەگوترێت و بە ماتریسەکانی $(m, 1)$ ئەستوون دەگوترێت. ئەم ماتریسە تایبەتانە هەروەها بە ڤێکتۆری ڕیز/ئەستوون ناو دەبرێن .

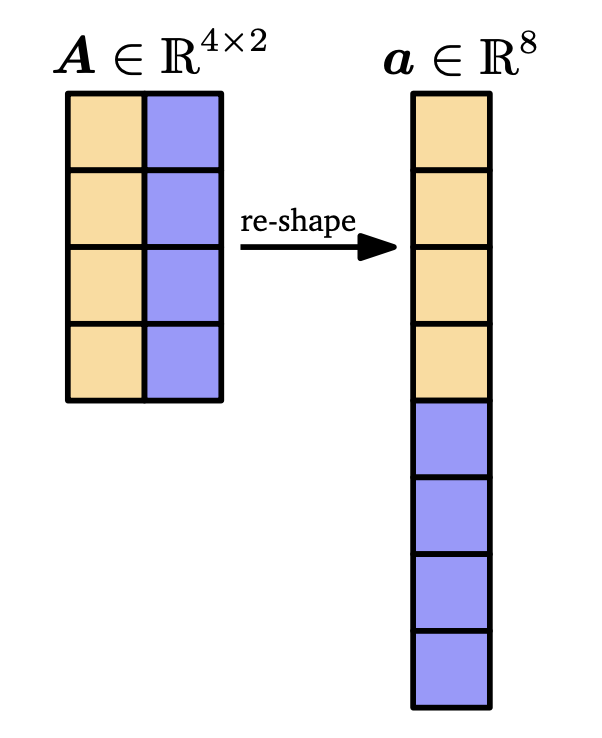
$\mathbb{R}^{m \times n}$ بریتییە لە کۆمەڵەی هەموو ماتریسەکانی ژمارەی ڕاستی $(m, n)$. $A \in \mathbb{R}^{m \times n}$ بە شێوەیەکی دیکەش $\mathbf{a} \in \mathbb{R}^{mn}$ بە سەریەکنانی $n$ ئەستوون لە ڤێتۆرێکی درێژدا پیشان دەدرێت.

نوێ دەکرێتەوە ...